Numbers
Page: 4 of 6
Proof that √2 is Irrational
Proof By Contradiction is a form of indirect proof, that establishes the truth of a proposition by showing that the proposition being false would imply a contradiction. Therefore, we assume that √2 is rational and that √2 can be written as a quotient.
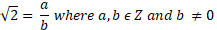
a⁄b is in the simplest form and so a and b are coprime
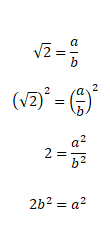
2b2 is an even number so 2 is a factor of a2
a2 is an even number so 2 is a factor of a
Let a = 2K where K ∈ Z
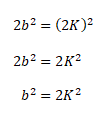
2K2 is an even number so 2 is a factor of b2
b2 is an even number so 2 is a factor of b
Hence 2 is a factor of both a and b
Therefore a⁄b is not in its simplest form
This contradicts the assumption that √2 can be written as a rational number in its simplest form
By proof by contradiction √2 is an irrational number