Numbers 1
Page: 6 of 6
Geometric Construction of √3
- Draw line segment [AB] of length 1 unit
- Construct a circle with a centre at A and a radius of [AB]
- Construct another circle with a centre at B and a radius of [AB]
- Mark the intersections of the two circles C, D
- Draw the line segment [CD]
- |CD| = √3
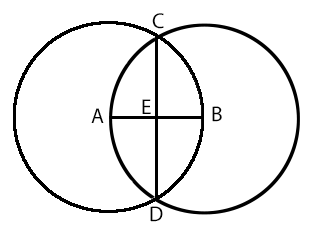
Proof:
- [CD] is the perpendicular bisector of [AB]
- |AE| = |EB| = 1⁄2
- |AC| = |BC|
- |AE|2 + |EC|2 = |AC|2 Pythagoras
- (1⁄2)2 + |EC|2 = 12
- 1⁄4 + |EC|2 = 1
- |EC|2 = 3⁄4
- |EC| = √3⁄4
- |EC| = √3⁄2
- |CD| = 2|EC|
- |CD| = 2 (√3⁄2)
- |CD| = √3